The SubGrad class implements the NDOSolver interface for NonDifferentiable Optimization Solvers [see NDOSlver.h], using a unified subgradient-type algorithm as described in:
More...
#include <SubGrad.h>
Public Types | |
Public Types | |
 Public Types inherited from NDOSolver Public Types inherited from NDOSolver |
Public Member Functions | |
Constructor | |
| SubGrad (istream *iStrm=0) | |
| Constructor of the class. More... | |
Other initializations | |
| void | SetStepsize (Stepsize *STP=0) |
Gives to the SubGrad object a pointer to an object of class Stepsize that will be used to provide 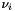 during the subgradient algorithm. More... during the subgradient algorithm. More... | |
| void | SetDeflection (Deflection *Vol=0) |
Gives to the SubGrad object a pointer to an object of class Deflection that will be used to provide a deflection coefficient 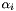 . More... . More... | |
| void | SetQKNP (CQKnPClass *KNP=0) |
| Gives to the SubGrad object a pointer to an object of class CQKnPClass that will be used as quadratic knapsack solver during the subgradient algorithm. More... | |
| void | SetFiOracle (FiOracle *Fi=0) |
| void | SetLambda (cLMRow tLambda=0) |
| void | KeepBestLambda (const bool KBL=true) |
| void | SetPar (const int wp, const int value) |
| Extends NDOSolver::SetPar( , cIndex ) for handling the SubGrad-specific parameters; the enum SGParam is used (in the obvious way) for selecting the parameter to be set. More... | |
| void | SetPar (const int wp, cHpNum value) |
| Extends NDOSolver::SetPar( , cHpNum ) for handling the SubGrad-specific parameters; the enum SGParam is used (in the obvious way) for selecting the parameter to be set. More... | |
| void | SetPar (const int wp, const bool value) |
| Change boolean algorithmic parameters of the SubGrad solver. More... | |
| void | SetNDOLog (ostream *outs=0, const char lvl=0) |
| lvl controls the "level of verbosity" of the code. More... | |
Solving the problem | |
| NDOStatus | Solve (void) |
| Tries to minimize the function [see NDOSlver.h]. More... | |
| void | ReSetAlg (unsigned char RstLvl=0) |
| Resets the internal state of the Subgradient algorithm. More... | |
Reading the solution | |
| cLMRow | ReadBestSol (cIndex_Set &I, Index &D) |
Returns a read-only pointer to the point having the lowest  value found so far [see below]. More... value found so far [see below]. More... | |
| HpNum | ReadBestFiVal (cIndex wFi=Inf< Index >()) |
Returns the best  value found so far. More... value found so far. More... | |
| cLMRow | ReadSol (cIndex_Set &I, Index &D) |
Returns a read-only pointer to the stability center 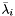 . More... . More... | |
| HpNum | ReadFiVal (cIndex wFi=Inf< Index >()) |
Independently from which "component" of Fi() is chosen, it returns the full function Fi at the stability center 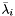 . . | |
| HpNum | ReadHatFiVal (void) |
Returns 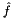 , if , if  is kept in memory. More... is kept in memory. More... | |
| bool | IsOptimal (HpNum eps=0) |
Returns true if the solution 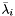 is is 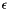 -optimal (relative), being -optimal (relative), being 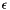 set to EpsLin. More... set to EpsLin. More... | |
| cHpRow | ReadMult (cIndex_Set &I, Index &D, cIndex wFi=Inf< Index >()) |
| HpNum | ReadLBMult (cIndex wFi=Inf< Index >()) |
Reading the data of the problem | |
| void | GetPar (const int wp, int &value) |
| void | GetPar (const int wp, HpNum &value) |
| void | GetPar (const int wp, bool &value) |
Adding / removing / changing data | |
| void | AddVariables (Index NNwVrs, cLMRow IVs=0) |
| void | RemoveVariables (cIndex_Set whch=0, Index hwmny=0) |
| void | ChgFiV (cIndex wFi=Inf< Index >()) |
| void | ChgSbG (cIndex strt=0, Index stp=Inf< Index >(), cIndex wFi=Inf< Index >()) |
Destructor | |
| ~SubGrad () | |
 Public Member Functions inherited from NDOSolver Public Member Functions inherited from NDOSolver | |
| virtual bool | IsOptimal (HpNum eps=0) const |
| This method should return true if the NDOSolver believes that the current solution [see ReadSol() above] is eps-optimal (relative). More... | |
| Index | FiEval (void) const |
| Returns the number of times that Fi() has been called; if called from within Fi(), the present call should be excluded. More... | |
| Index | GiEval (void) const |
| Returns the number of times that NewGi() has been called; if called from within NewGi(), the present call should be excluded. More... | |
| Index | NrCalls (void) const |
| Returns the number of times that Solve() has been called; if called from within Solve(), the present call should be included. More... | |
| Index | NrIter (void) const |
| Returns the current number of iterations. More... | |
| void | NDOTime (double &t_us, double &t_ss) |
| If this method is called within any of the methods of the class that are "actively timed" (this depends on the subclasses), it returns the user and sistem time (in seconds) since the start of that method. More... | |
| double | NDOTime (void) |
| As NDOTime( double & , double & ) [see above], except that returns the total (system + user ) time. More... | |
| NDOSolver (istream *iStrm=0) | |
| Constructor of the class. More... | |
| virtual void | SetNDOTime (const bool TimeIt=true) |
| SetNDOTime() allocates an OPTtimers object [see OPTUtils.h] that should be used for timing the calls to relevant methods of the class. More... | |
| Index | GetNumVar (void) const |
| Returns the current number of variables of the function; a protected field is offered by the base class to keep this information. More... | |
| virtual | ~NDOSolver () |
| Destructor of the class. More... | |
Protected Member Functions | |
| void | FiAndGi (cIndex wFi=Inf< Index >()) |
Evaluates the function at the new point 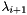 , i.e., , i.e., 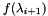 , and it either computes a subgradient , and it either computes a subgradient 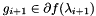 , or, if the point is infeasible, a constraint. More... , or, if the point is infeasible, a constraint. More... | |
| void | FormD (void) |
The method is used within Solve() [see above], and its job is to compute the direction  that appears in the formula of that appears in the formula of 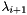 . More... . More... | |
| void | SaveDir (void) |
| The method is combined with FormD() [see above] to carry out the direction computation. More... | |
| void | GotoLambda1 (void) |
Move the current point to 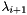 . More... . More... | |
| void | FormLambda1 (void) |
After a (succesfull) call to FormD(), sets the new (unprojected) tentative point 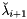 as as
Remark that the point | |
Protected Attributes | |
| Index | SGPar1 |
| projection-strategy parameters | |
| HpNum | SGPar2 |
| incremental factor | |
| Index | SGPar3 |
| scheme: stepsize(deflection)-restricted | |
| bool | SGPar4 |
control if  is kept is kept | |
| Index | SGPar5 |
| seed | |
| Stepsize * | stepsize |
| pointer to the Stepsize class | |
| Deflection * | deflection |
| pointer to the Deflection class | |
| CQKnPClass * | Q2KNP |
| pointer to the quadratic knapsack solver | |
| Index | MaxNumVar |
| maximum number of variables | |
| Index | MaxNConst |
| maximum number of simplex constraints | |
| bool | BoxConst |
| true, if there are some box constraints | |
| LMRow | LambdaBar |
the stability center 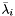 | |
| HpNum | FiBar |
| full function value at LambdaBar | |
| LMRow | Lambda |
the current point 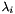 or the trial point or the trial point 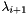 | |
| HpNum | FiLambda |
| full function value at Lambda | |
| LMRow | LambdaHat |
the point  | |
| HpNum | FiHat |
| full function value at HLmb | |
| bool | LHasChgd |
| true if Lambda has changed since the latest call to FiAndGi() | |
| bool | LHasProj |
| true if Lambda has projected in the current iteration | |
| bool | KpBstL |
| if LambdaBest has to be kept | |
| HpNum | FiBest |
the best value of  found so far found so far | |
| LMRow | LambdaBest |
| the best point found so far | |
| HpNum | LowerBound |
Lower Bound over the full function  . . | |
| bool | TrueLB |
| true if LowerBound is a "true" lower bound rather than just the "minus infinity" | |
| SgRow | Gi |
| Gi[ wFi ]( Lambda ), the subgradient. | |
| SgRow | dir |
the direction 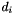 | |
| HpNum | alpha |
the deflection parameter 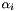 | |
| HpNum | step |
the stepsize 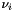 | |
| HpNum | Sigma |
the linearization error 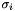 of of 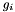 at at 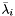 | |
| HpNum | Epsilon |
the linearization error 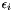 of of  at at 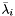 | |
| HpNum | SigmaHat |
the linearization error 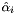 of of 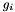 with respect to with respect to 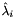 | |
| HpNum | HatEpsilon |
the linearization error 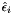 of of  with respect to with respect to 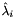 | |
| Index_Set | SGBase |
| the set of indices of Gi[ wFi ]( Lambda ) | |
| Index | MaxName |
| maximum name to be used in FiOracle->SetGiName() | |
| HpNum | NrmGi |
| the (squared) subgradient's norm | |
| HpNum | NrmDir |
| the (squared) direction's norm | |
| HpNum | dGk |
scalar product between  and and 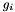 | |
| HpNum | dM1Gk |
scalar product between  and and 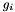 | |
| bool | dM1GkDone |
true if the scalar product 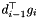 has been computed has been computed | |
| Index_Set | CnstBeg |
| CnstBeg and CnstVol point respectively to a MaxNConst-vector of Index and HpNum, while CnstNxt is a MaxNumVar-vector of SIndex. More... | |
| HpRow | CnstVol |
| the MaxNConst-vector of HpNum containing the rhs of the knapsack Constraints | |
| SIndex_Set | CnstNxt |
| the MaxNumVar-vector of SIndex saying the next variable appearing in a knapsack constraint [see above] | |
| LMRow | ub |
| upper bounds on the variables | |
| LMRow | lb |
| lower bounds on the variables | |
| bool | ZeroComp |
| true if Fi() comes with the 0-th component | |
| Index | NItIncr |
| number of incremental iterations after an outer iteration | |
| bool | InnIter |
| if true, the current iteration is an inner one | |
| vector< Index > | Seq |
vector containing the randomly shuffled components of the function  | |
| bool | DirPos |
indicates where the direction  in located in the oracle in located in the oracle | |
| Index | CSSCntr |
| counter of consecutive SS | |
| Index | CNSCntr |
| counter of consecutive NS | |
| Index | CSmallStep |
| counter of consecutive short step | |
| bool | DoSS |
| SS vs NS. | |
| FiOracle::FiStatus | fs |
| FiOracle status. | |
| bool | EmptySet |
| true, if the feasible set is empty | |
 Protected Attributes inherited from NDOSolver Protected Attributes inherited from NDOSolver | |
| FiOracle * | Oracle |
| (pointer to) the oracle for Fi | |
| Index | MaxIter |
| maximum number of iterations | |
| HpNum | MaxTime |
| maximum time (in seconds) for each call to Solve() | |
| HpNum | tStar |
| optimality related parameter: "scaling" of Fi | |
| HpNum | EpsLin |
| optimality related parameter: relative precision | |
| HpNum | EInit |
| precision-related parameter: initial precision | |
| HpNum | EFnal |
| precision-related parameter: final precision | |
| HpNum | EDcrs |
| precision-related parameter: rate of decrease | |
| int | EStps |
| precision-related parameter: number of steps | |
| NDOStatus | Result |
| result of the latest call to Solve() | |
| Index | NumVar |
| (current) number of variables | |
| Index | NrFi |
| number of components of Fi() | |
| Index | SCalls |
| nuber of calls to Solve() (the current included) | |
| Index | ParIter |
| nuber of iterations in this run | |
| Index | FiEvaltns |
| total number of Fi() calls | |
| Index | GiEvaltns |
| total number of Gi() calls | |
| ostream * | NDOLog |
| the output stream object for log purposes | |
| char | NDOLLvl |
| the "level of verbosity" of the log | |
| OPTtimers * | NDOt |
| OPTtimer for timing purposes. | |
Friends | |
Friend classes | |
| class | Stepsize |
| The classes Stepsize and Deflection are "friends" of SubGrad. More... | |
| class | Deflection |
Detailed Description
The SubGrad class implements the NDOSolver interface for NonDifferentiable Optimization Solvers [see NDOSlver.h], using a unified subgradient-type algorithm as described in:
A. Frangioni, E. Gorgone, B. Gendron. On the Computational Efficiency of Subgradient Methods: A Case Study in Combinatorial Optimization. Technical Report CIRRELT- 2015-41, Interuniversity Research Centre on Enterprise Networks, Logistics and Transportation (CIRRELT), Montreal, Canada, 2015
This is in fact a subgradient method (SM) based on abstract rules for the computation of both the stepsize 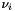 and the direction
and the direction  . The algorithm in employs the simple recurrence formula:
. The algorithm in employs the simple recurrence formula:
![\[ \breve{\lambda}_{i+1} \gets \bar{\lambda}_i - \nu_i d_i \quad , \quad \lambda_{i+1} \gets {\rm P}_{\Lambda}( \, \breve{\lambda}_{i+1} \, ) \]](form_60.png)
where 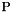 denotes the orthogonal projection on
denotes the orthogonal projection on 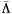 . The point
. The point 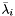 is not necessarily the current iterate. For instance, it could be required that
is not necessarily the current iterate. For instance, it could be required that 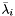 remains unchanged if an ascent direction occurs. It recalls somehow the stability center of the bundle methods.
remains unchanged if an ascent direction occurs. It recalls somehow the stability center of the bundle methods.
The class relies on the objects of the friend classes Stepsize and Deflection, which have to return, respectively, the stepsize 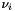 and the deflection coefficient
and the deflection coefficient 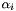 . The latter scalar number defines in turn the direction
. The latter scalar number defines in turn the direction  , i.e..
, i.e.. 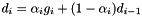 . These abstract classes allow us to derive several variants of the method. For the sake of simplicity, the original SM characterized by
. These abstract classes allow us to derive several variants of the method. For the sake of simplicity, the original SM characterized by  is performed setting the pointer to the object Deflection to NULL.
is performed setting the pointer to the object Deflection to NULL.
The class also includes the incremental variant for when the function to be maximized is composed by a sum of different functions.
Member Enumeration Documentation
| enum SGParam |
Public enum which "extends" the enum NDOSolver::NDOParam for handling the SubGrad-specific algorithmic parameters in (the two overloaded versions of) SubGrad::SetPar() [see below].
Constructor & Destructor Documentation
| SubGrad | ( | istream * | iStrm = 0 | ) |
Constructor of the class.
The parameter `iStrm', if provided, is taken as a pointer to a istream from which the algorithmic parameters for the subgradient algorithm are sequentially read in the following order. Each parameter must be placed at the beginning of a separate line, max 255 characters long, with all the rest of the line up to the first newline character (apart from a separating whitespace) being available for comments. Any line whose first character is '#' and any blank line is ignored. If 0 is passed, the file ends before reaching a given parameter, or some parameter is in the wrong format, each non-specified parameter is given a default value, shown in [] below.
`iStrm' is passed to the constructor of NDOSolver [see NDOSolver.h], which reads the general algorithmic parameters out of it; since the constructor SubGrad is executed after the one of NDOSolver, the following parameters specific for the SubGrad have to be found in the stream after those of the base class:
Index SGPar1 [0] The direction
 is assumed to be such a convex combination of the subgradient
is assumed to be such a convex combination of the subgradient 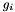 and the direction
and the direction  :
: ![\[ d_i = \alpha_i g_i + ( 1 - \alpha_i ) d_{i-1} \]](form_69.png)
SGPar1 selects among
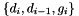 the vector(s) to be projected over the tangent cone at
the vector(s) to be projected over the tangent cone at 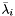 . The field SGPar1 is coded bit-wise, in the following way:
. The field SGPar1 is coded bit-wise, in the following way:- bit 0: if 1 the subgradient
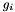 is projected, 0 otherwise;
is projected, 0 otherwise; - bit 1: if 1 the direction
 is projected, 0 otherwise;
is projected, 0 otherwise; - bit 2: if 1 the
 is projected, 0 otherwise;
is projected, 0 otherwise;
The setting (+7) is redundant. In fact, it is equivalent to (+3) because
 , being a (convex) combination of
, being a (convex) combination of 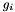 and
and  , coincides with its projection.
, coincides with its projection.- bit 0: if 1 the subgradient
- HpNum SGPar2 [0] To manage the incremental iterations. A sequence of incremental (or inner) iterations NItIncr performed along single-component subgradients could occur before a full (or normal, or outer) iteration. The number NItIncr is obtained as NItIncr = ceil( <Number of components of
 > * SGPar2 ), where the number of components of
> * SGPar2 ), where the number of components of  includes the 0-th component, and then not necessarily coincides with NrFi. Finally, the incremental variant only works with no deflection object, i.e setting deflection = NULL, because we do not manage with the sum of subgradients of different components.
includes the 0-th component, and then not necessarily coincides with NrFi. Finally, the incremental variant only works with no deflection object, i.e setting deflection = NULL, because we do not manage with the sum of subgradients of different components. - Index SGPar3 [1] The convergence scheme. This field is coded bit-wise in the following way:
- bit 0: 1 if the safe rule is used, 0 otherwise
- bit 1: 1 for the stepsize-restricted scheme, 0 for the deflection-restricted scheme.
- bool SGPar4 [true] SGPar4 enables the use of
which could have a certain influence on the stopping test [see IsOptimal()].![\[ \hat{\lambda}_{i+1} = \alpha_{i+1}\lambda_i + ( 1 - \alpha_{i+1} ) \hat{\lambda}_i \]](form_73.png)
- Index SGPar5 [0] The seed value used in a call to srand. The components are re-shuffled in the incrmental variant, and a random number generator is used.
Member Function Documentation
| void SetStepsize | ( | Stepsize * | STP = 0 | ) |
Gives to the SubGrad object a pointer to an object of class Stepsize that will be used to provide 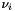 during the subgradient algorithm.
during the subgradient algorithm.
The Stepsize object can be changed during the life of a SubGrad object, but this change clearly forces the reset of all the information about the function accumulated so far. Passing a 0 pointer does exactly this job.
| void SetDeflection | ( | Deflection * | Vol = 0 | ) |
Gives to the SubGrad object a pointer to an object of class Deflection that will be used to provide a deflection coefficient 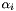 .
.
The Deflection object can be changed during the life of a SubGrad object, but this change clearly forces the reset of all the information about the function accumulated so far. Passing a 0 pointer does exactly this job.
In addition, 0 pointer means that the deflection coefficient is kept to 1, namely  .
.
| void SetQKNP | ( | CQKnPClass * | KNP = 0 | ) |
Gives to the SubGrad object a pointer to an object of class CQKnPClass that will be used as quadratic knapsack solver during the subgradient algorithm.
CQKnPClass object is employed to project the subgradient/direction when the projection problem is a continuous quadratic knapsack one. Moreover, the data of the problem are fixed just before the projection, hence no information is kept in the Subgradient method.
The CQKnPClass object can be changed during the life of a SubGrad object, but this change clearly implies that the prior object must be discharged. Passing a 0 pointer does exactly this job.
The default implementation assigns zero to the pointer of the CQKnPClass object directly in the constructor. In fact, CQKnPClass solver comes be helpful whenever in the feasible set the knapsack constraints appear. In contrast to what happens in both SetStepsize() and SetDeflection(), the call to the function SetQKNP() is mandatory only if knapsack constraints take place in the feasible set.
|
virtual |
Extends NDOSolver::SetPar( , cIndex ) for handling the SubGrad-specific parameters; the enum SGParam is used (in the obvious way) for selecting the parameter to be set.
Reimplemented from NDOSolver.
|
virtual |
Extends NDOSolver::SetPar( , cHpNum ) for handling the SubGrad-specific parameters; the enum SGParam is used (in the obvious way) for selecting the parameter to be set.
Reimplemented from NDOSolver.
| void SetPar | ( | const int | wp, |
| const bool | value | ||
| ) |
Change boolean algorithmic parameters of the SubGrad solver.
The enum SGParam [see above] is used for selecting the parameter to be set.
|
virtual |
lvl controls the "level of verbosity" of the code.
The first four bits of lvl have the following meaning:
- 0 => no log at all (also assumed if log = 0);
- 1 => "basic" log: only the errors are reported;
- 2 => a detailed step-by-step log of the algorithm is displayed;
- 4 .. 15 unused, available to derived classes;
Reimplemented from NDOSolver.
|
virtual |
Tries to minimize the function [see NDOSlver.h].
It implements the subgradient algorithm exploiting the protected methods FormD(), SaveDir(), FormLambda1(), FiAndGi(), GotoLambda1() [see below].
Returns if
- kOK optimization has been succesful: a solution that is "optimal" (w.r.t. the current parameters settings) has been found;
- kUnbndd there has been an error in the FiOracle, i.e. Fi() has returned -HpINF, or the function is unbounded below: the latter case can be detected only if a lower bound on the min. value of
 is available [see FiOracle::GetMinusInfinity()];
is available [see FiOracle::GetMinusInfinity()]; - kUnfsbl the polyhedral set defined by the constraints is empty: in this case, the primal optimal solution is an unbounded extreme ray for the dual problem;
- kStopped Solve() has been stopped, either by FiOracle::GetFiStatus() or because the stepsize has been "too small" during 100 consecutive outer iterations [or 100 * NrFi consecutive inner iterations];
- kStpIter the max. number of iterations has been exhausted;
- kStpTime the max. running time has been reached;
- kError There have been some problem in the FiOracle that require to stop the optimization.
As for kStopped, "too small" means that 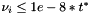 , where
, where 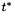 is the optimality related parameter scaling Fi() [see NDOSlver.h]. There is no reason, in principle, why we couldn't replace
is the optimality related parameter scaling Fi() [see NDOSlver.h]. There is no reason, in principle, why we couldn't replace 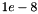 by a parameter, but in order to make the test easier this parameter has been fixed to
by a parameter, but in order to make the test easier this parameter has been fixed to 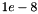 . We also decided to replace by 100 the parameter saying how many outer iterations of consecutive small stepsizes are sufficient to stop the algorithm.
. We also decided to replace by 100 the parameter saying how many outer iterations of consecutive small stepsizes are sufficient to stop the algorithm.
Note that, whatever the exit condition be, the current point is always available by calling ReadSol(), and its Fi() value by calling ReadFiVal() [see below].
Implements NDOSolver.
|
virtual |
Resets the internal state of the Subgradient algorithm.
Since several different things can be reset independently, RstLvl is coded bit-wise:
- bit 0: if 0 all the algorithmic parameters are reset to the default values read by the stream/set by SetPar(), while if 1 they are left untouched;
- bit 1: if 0 the current point is reset to the all-0 vector, while if 1 it is left untouched;
- bit 2: if 0 the direction and the subgradient are removed, while if 1 they are left there;
- bit 3: if 0 all the constraints are removed, while if 1 all of them are left there.
- bit 4: if 0 the value of Fi() in the stability center is reset to INF (i.e., unknown), while if 1 it is left untouched.
Reimplemented from NDOSolver.
|
virtual |
Returns a read-only pointer to the point having the lowest  value found so far [see below].
value found so far [see below].
Reimplemented from NDOSolver.
|
virtual |
Returns the best  value found so far.
value found so far.
Independently from which "component" of Fi() is chosen, it returns the full function.
Reimplemented from NDOSolver.
Referenced by ColorTV::ColorTV().
|
virtual |
Returns a read-only pointer to the stability center 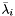 .
.
If Solve() has returned a kOK and the tStar has been properly set, the point returned by ReadSol() - and, a fortiori, the one returned by ReadBestSol() - is 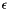 -optimal.
-optimal.
Implements NDOSolver.
| HpNum ReadHatFiVal | ( | void | ) |
Returns 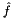 , if
, if  is kept in memory.
is kept in memory.
Otherwise it returns Inf<HpNum>().
| bool IsOptimal | ( | HpNum | eps = 0 | ) |
Returns true if the solution 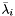 is
is 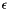 -optimal (relative), being
-optimal (relative), being 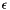 set to EpsLin.
set to EpsLin.
The parameter SGPar4 controls the linearization error to be used in the stopping condition:
- SGPar4 = true:
![\[ t^* \|d_i\| + \max\{ \hat{\epsilon}_i , \epsilon_i \} <= \epsilon * max( 1 , |f_i^{rec}| ) \]](form_82.png)
SGPar4 = false: The criteria is just
![\[ t^* \|d_i\| + \epsilon_i <= \epsilon * max( 1 , |f_i^{rec}| ) \]](form_83.png)
where
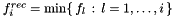 , i.e. the record value on the optimum $f_*$
, i.e. the record value on the optimum $f_*$
|
protected |
Evaluates the function at the new point 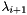 , i.e.,
, i.e., 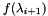 , and it either computes a subgradient
, and it either computes a subgradient 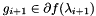 , or, if the point is infeasible, a constraint.
, or, if the point is infeasible, a constraint.
|
protected |
The method is used within Solve() [see above], and its job is to compute the direction  that appears in the formula of
that appears in the formula of 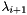 .
.
The direction is actually saved after the variables generation because (i) the subgradient keeps in memory just the current direction (ii) by generating/removing variables the direction may quickly come to be deteriorated. When the variables generation is ended [see GetFiStatus() in FiOracle.h], SaveDir() must be called in order to update the direction.
In addition, the deflection coefficient is computed inside FormD(). As for the stepsize, the computation is performed within FormD() only if the scheme is deflection-restricted.
|
protected |
|
protected |
Move the current point to 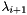 .
.
|
protected |
After a (succesfull) call to FormD(), sets the new (unprojected) tentative point 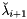 as
as
![\[ \breve{\lambda}_{i+1} = \lambda_i - \nu_i d_i \,. \]](form_89.png)
Remark that the point 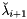 must be projected before calling FiandGi() [see above], i.e.,
must be projected before calling FiandGi() [see above], i.e., 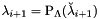 .
.
Friends And Related Function Documentation
|
friend |
The classes Stepsize and Deflection are "friends" of SubGrad.
This is done because Stepsize and Deflection objects may need some protected data to work. An issue, however, is that derived classes from friend classes are not friend, and therefore actual implementations of Stepsize and Deflection cannot access data of SubGrad unless this capability is explicitly provided by the base classes, who are friends. This is why Stepsize and Deflection define a few methods that allow to read protected data of SubGrad: so that any derived class can use them to access to these data. These methods are, in fact, implemented at the end of SubGrad.C.
Member Data Documentation
|
protected |
CnstBeg and CnstVol point respectively to a MaxNConst-vector of Index and HpNum, while CnstNxt is a MaxNumVar-vector of SIndex.
Each variable is associated to one and only knapsack constraint. CnstVol[ i ] is the volume of the i-th knapsack constraint. CnstBeg[ i ] supplies the starting of the i-th constraint, i.e. the first variable entering the i-th knpasack constraint. CnstNxt[ j ] says the name of the next variable to j entering the same knapsack constraint. If CnstNxt[ j ] == MaxNumVar, then no other variable enters that knapsack constraint, and if CnstNxt[ j ] == -1, the variable does not belong to any knapsack constraint.
