The class ContQKsk defines an interface for Continuous Quadratic Knapsack problems (CQKnP) solvers. More...

#include <CQKnPClass.h>

Inheritance diagram for CQKnPClass:

Classes
class	CQKException
	Small class for exceptions. More...

class	Inf
	Small class using std::numeric_limits to extract the "infinity" value of a basic type (just use Inf<type>()). More...

Public Types
Public types

Public Member Functions
virtual void	LoadSet (const int pn=0, const double pC=0, const double pD=0, const double pA=0, const double pB=0, const double pV=0, const bool sns=true)=0
	Inputs a new CQKnP instance. More...

virtual void	ReadInstance (std::istream &inFile, bool RBV=false)
	Read the instance from file. More...

virtual void	SetEps (const double eps=1e-6)=0
	Defines the precision required to construct the solution of the knapsack problem. More...

virtual CQKStatus	SolveKNP (void)=0
	SolveKNP() attempts to solve the current CQKnP instance, returning the status indicating the outcome of the optimization. More...

virtual const double *	KNPGetX (void)=0
	Return the best feasible solution of the CQKnP found so far (assuming CheckFsb() == true, see above), which is optimal if SolveKNP() has returned kOK (see above). More...

virtual double	KNPGetPi (void)=0
	Returns the optimal dual multiplier of the knapsack constraint; the returned value is dependable only if SolveKNP() has returned kOK (see above). More...

virtual double	KNPGetFO (void)=0
	Returns the optimal value of the objective function of the problem. More...

virtual int	KNPn (void)
	Returns the current number of items. More...

virtual void	KNPLCosts (double csts, const int nms=0, int strt=0, int stp=Inf< int >())=0
	The linear costs of the items are written into csts[]. More...

virtual void	KNPQCosts (double csts, const int nms=0, int strt=0, int stp=Inf< int >())=0
	The quadratic costs of the items are written into csts[]. More...

virtual double	KNPLCost (const int i)=0
	Return the linear cost of the i-th item (i = 0 . More...

virtual double	KNPQCost (const int i)=0
	Return the quadratic cost of the i-th item (i = 0 . More...

virtual void	KNPLBnds (double bnds, const int nms=0, int strt=0, int stp=Inf< int >())=0
	The lower bounds of the items are written into bnds[]. More...

virtual void	KNPUBnds (double bnds, const int nms=0, int strt=0, int stp=Inf< int >())=0
	The upper bounds of the items are written into bnds[]. More...

virtual double	KNPLBnd (const int i)=0
	Return the lower bound of the i-th item (i = 0 . More...

virtual double	KNPUBnd (const int i)=0
	Return the upper bound of the i-th item (i = 0 . More...

virtual double	KNPVlm (void)=0
	Returns the volume `V' of the knapsack. More...

virtual void	WriteInstance (std::ostream &oFile, const int precc=16, const int precv=16)
	Write the instance to the provided ostream in the "complete" format read by ReadInstance() [see above]. More...

virtual void	ChgLCosts (const double csts, const int nms=0, int strt=0, int stp=Inf< int >())=0
	Change the linear cost coefficients that are: More...

virtual void	ChgQCosts (const double csts, const int nms=0, int strt=0, int stp=Inf< int >())=0
	Change the quadratic cost coefficients that are: More...

virtual void	ChgLCost (int i, const double cst)=0
	Change the linear cost coefficient of item i to cst. More...

virtual void	ChgQCost (int i, const double cst)=0
	Change the quadratic cost coefficient of item i to cst. More...

virtual void	ChgLBnds (const double bnds, const int nms=0, int strt=0, int stp=Inf< int >())=0
	Change the item lower bounds that are: More...

virtual void	ChgUBnds (const double bnds, const int nms=0, int strt=0, int stp=Inf< int >())=0
	Change the item upper bounds that are: More...

virtual void	ChgLBnd (int i, const double bnd)=0
	Change the lower bound of item i to bnd. More...

virtual void	ChgUBnd (int i, const double bnd)=0
	Change the upper bound of item i to bnd. More...

virtual void	ChgVlm (const double NVlm)=0
	Change the volume. More...

Protected Attributes
int	n
	total number of items

int	status
	status of the algorithm: it is an int so that derived classes can use it to encode other information apart from the return value of SolveKNP(). More...

Detailed Description

The class ContQKsk defines an interface for Continuous Quadratic Knapsack problems (CQKnP) solvers.

The data of the problem consists of a set of items = ( 0 , ... , n - 1 ), where each item i has:

a linear cost C[ i ];
a quadratic cost D[ i ] $\in R_+$ ;
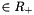a lower bound A[ i ] $\in R \cup$ -INF, and
an upper bound B[ i ] $\in R \cup$ +INF.

The problem requires to find the most valuable set of items which fit in a knapsack of given volume V, but partly accepting items is allowed. The formulation of the problem is therefore:

$\min \sum_{i \in E} C[ i ] * X[ i ] + D[ i ] * X[ i ]^2$

$\sum_{i \in E} X[ i ] \leq V ( = V )$

$A[ i ] \leq X[ i ] \leq B[ i ] \hspace{1cm} i \in E$

This is a convex quadratic problem, hence a "easy" one. However it is repeatedly solved as a subproblem in many applications, so a fast solver may ultimately be useful.

Member Enumeration Documentation

enum CQKStatus

Public enum describing the possible status of the MCF solver.

Enumerator
kOK	optimal solution found
kStopped	optimization stopped
kUnfeasible	problem is unfeasible
kUnbounded	problem is unbounded
kError	error in the solver
kUnSolved	no solution available yet

Member Function Documentation

virtual void LoadSet	(	const int	pn = `0`,
		const double *	pC = `0`,
		const double *	pD = `0`,
		const double *	pA = `0`,
		const double *	pB = `0`,
		const double	pV = `0`,
		const bool	sns = `true`
	)

pure virtual

Inputs a new CQKnP instance.

The meaning of the parameters is the following:

pn is the current number of items of the set: passing pn == 0 is intended as a signal to the solver to deallocate everything and wait for new orders; in this case, all the other parameters are ignored.
pC is the n-vector of the linear part of item costs; the linear costs must be finite (- INF < pC[ i ] < INF); pC == 0 means that all linear costs are 0.
pD is the n-vector of the quadratic part of item costs; the quadratic costs must be non-negative and finite (0 <= pD[ i ] < INF); pD == 0 means that all quadratic costs are 0.
pA is the n-vector of the item lower bounds; lower bound must be < + INF; pA == 0 means that all lower bound are - INF.
pB is the n-vector of the item upper bounds; upper bounds must be > -INF; pB == 0 means that all upper bounds are + INF.
pV is the knapsack volume, which must be finite (- INF < pV < + INF).
sns is the sense of knapsack constraint: true is for an equality constraint (default), false for an inequality (<=) constraint.

This method must be called prior to invoking any other method of the class, with the exception of SetKNPLog() and SetEps() (not to mention the constructor, of course).

Referenced by CQKnPClass::ReadInstance().

void ReadInstance	(	std::istream &	inFile,
		bool	RBV = `false`
	)

inlinevirtual

Read the instance from file.

While virtual, the method is implemented in the base class: the instance data is read in temporary data structures and then LoadSet() [see above] is called using these. Thus, the method will work for any derived class with no modification, since it uses the class-provided implmentation of LoadSet(); however, being virtual it can be re-implemented for maximum efficiency if desired.

The method supports two formats of the file: a "simplified" one and a "complete" one. The simplified format, assumed when RBV is false, is:

for i = 0 to n - 1 <linear cost="" of="" item="" i>="">

for i = 0 to n - 1 <quadratic cost="" of="" item="" i>="">

In this case all lower bounds are zero, all upper bounds are INF, and the volume is 1. Otherwise (RBV == true) the file must continue with

for i = 0 to n - 1 <lower bound="" of="" item="" i>="">

for i = 0 to n - 1 <upper bound="" of="" item="" i>="">

Note that this method is "alternative" to LoadSet() (in the sense that the latter is invoked inside), so the object is "ready to use" once this method returns.

References CQKnPClass::LoadSet().

virtual void SetEps ( const double eps = 1e-6 )

pure virtual

Defines the precision required to construct the solution of the knapsack problem.

virtual CQKStatus SolveKNP ( void )

pure virtual

SolveKNP() attempts to solve the current CQKnP instance, returning the status indicating the outcome of the optimization.

Possible values are:

kUnSolved SolveKNP() has not been called yet, or the data of the problem has been changed since the last call;
kOK optimization has been carried out succesfully;
kStopped optimization have been stopped before that the stopping conditions of the solver applied, e.g. because of the maximum allowed number of "iterations" have been reached; this is not necessarily an error, as it might just be required to re-call SolveKNP() giving it more "resources" in order to solve the problem;
kUnfeasible the current CQKnP instance is (primal) unfeasible;
kUnbounded if the current CQKnP instance is (primal) unbounded: this can only happen if some of the items have +/-INF bounds and zero quadratic cost.
kError there was an error during the optimization; this typically indicates that computation cannot be resumed, although solver-dependent ways of dealing with solver-dependent errors may exhist.

virtual const double* KNPGetX ( void )

pure virtual

Return the best feasible solution of the CQKnP found so far (assuming CheckFsb() == true, see above), which is optimal if SolveKNP() has returned kOK (see above).

virtual double KNPGetPi ( void )

pure virtual

Returns the optimal dual multiplier of the knapsack constraint; the returned value is dependable only if SolveKNP() has returned kOK (see above).

virtual double KNPGetFO ( void )

pure virtual

Returns the optimal value of the objective function of the problem.

The method typically returns INF if SolveKNP() == kUnfeasible. It returns a finite feasible value if SolveKNP() == kOK or SolveKNP() == kStopped, but in the latter case it depends on the solver whether this is a lower or an upper bound on the optimal value. The return value is undefined in all other cases.

virtual int KNPn ( void )

inlinevirtual

Returns the current number of items.

The class has its protected field for storing this information, so this method is not pure virtual, but it is indeed virtual to allow re-definition if needed.

References CQKnPClass::ChgLBnd(), CQKnPClass::ChgLBnds(), CQKnPClass::ChgLCost(), CQKnPClass::ChgLCosts(), CQKnPClass::ChgQCost(), CQKnPClass::ChgQCosts(), CQKnPClass::ChgUBnd(), CQKnPClass::ChgUBnds(), CQKnPClass::ChgVlm(), CQKnPClass::KNPLBnd(), CQKnPClass::KNPLBnds(), CQKnPClass::KNPLCost(), CQKnPClass::KNPLCosts(), CQKnPClass::KNPQCost(), CQKnPClass::KNPQCosts(), CQKnPClass::KNPUBnd(), CQKnPClass::KNPUBnds(), CQKnPClass::KNPVlm(), CQKnPClass::n, and CQKnPClass::WriteInstance().

virtual void KNPLCosts	(	double *	csts,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

The linear costs of the items are written into csts[].

If nms == 0 then all the costs are written into csts[], otherwise cst[ i ] contains the informations relative to item nms[ i ] (nms must be Inf<int>()-terminated).

The parameters `strt' and `stp' allow to restrict the output of the method to all and only the items `i' with strt <= i < min( KNPn() , stp ). `strt' and `stp' work in "&&" with nms; that is, if nms != 0 then only the values corresponding to items which are both in nms and whose index is in the correct range are returned.

Referenced by CQKnPClass::KNPn().

virtual void KNPQCosts	(	double *	csts,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

The quadratic costs of the items are written into csts[].

If nms == 0 then all the costs are written into csts[], otherwise csts[ i ] contains the informations relative to item nms[ i ] (nms must be Inf<int>()-terminated).

The parameters `strt' and `stp' allow to restrict the output of the method to all and only the items `i' with strt <= i < min( KNPn() , stp ). `strt' and `stp' work in "&&" with nms; that is, if nms != 0 then only the values corresponding to items which are both in nms and whose index is in the correct range are returned (see above).

Referenced by CQKnPClass::KNPn().

virtual double KNPLCost ( const int i )

pure virtual

Return the linear cost of the i-th item (i = 0 .

. n - 1).

Referenced by CQKnPClass::KNPn(), and CQKnPClass::WriteInstance().

virtual double KNPQCost ( const int i )

pure virtual

Return the quadratic cost of the i-th item (i = 0 .

. n - 1).

Referenced by CQKnPClass::KNPn(), and CQKnPClass::WriteInstance().

virtual void KNPLBnds	(	double *	bnds,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

The lower bounds of the items are written into bnds[].

If nms == 0 then all the bounds are written, otherwise bnds[ i ] contains the information relative to item nms[ i ] (nms must be Inf<int>()-terminated).

The parameters `strt' and `stp' allow to restrict the output of the method to all and only the items `i' with strt <= i < min( KNPn() , stp ). `strt' and `stp' work in "&&" with nms; that is, if nms != 0 then only the values corresponding to items which are both in nms and whose index is in the correct range are returned.

Referenced by CQKnPClass::KNPn().

virtual void KNPUBnds	(	double *	bnds,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

The upper bounds of the items are written into bnds[].

If nms == 0 then all the bounds are written, otherwise bnds[ i ] contains the information relative to item nms[ i ] (nms must be Inf<int>()-terminated).

The parameters `strt' and `stp' allow to restrict the output of the method to all and only the items `i' with strt <= i < min( KNPn() , stp ). `strt' and `stp' work in "&&" with nms; that is, if nms != 0 then only the values corresponding to items which are both in nms and whose index is in the correct range are returned (see above).

Referenced by CQKnPClass::KNPn().

virtual double KNPLBnd ( const int i )

pure virtual

Return the lower bound of the i-th item (i = 0 .

. n - 1).

Referenced by CQKnPClass::KNPn(), and CQKnPClass::WriteInstance().

virtual double KNPUBnd ( const int i )

pure virtual

Return the upper bound of the i-th item (i = 0 .

. n - 1).

Referenced by CQKnPClass::KNPn(), and CQKnPClass::WriteInstance().

virtual double KNPVlm ( void )

pure virtual

Returns the volume `V' of the knapsack.

Referenced by CQKnPClass::KNPn(), and CQKnPClass::WriteInstance().

void WriteInstance	(	std::ostream &	oFile,
		const int	precc = `16`,
		const int	precv = `16`
	)

inlinevirtual

Write the instance to the provided ostream in the "complete" format read by ReadInstance() [see above].

The parameter "precc" and "precv" allow to set the precision (number of decimal digits) of the costs (linear and quadratic) and the bounds (upper and lower) and volume, respectively, when printed to the ostream. Rhe default value is "all digits of a double", which results in pretty large files, but smaller precisions are possible if one e.g. knows that the instance data is integer. Since this can typically be different for costs-related and volume-related information, two different parameters are provided.

While virtual, the method is implemented in the base class: the instance data is read from the object using the class-provided implmentation of KNPLCost(), KNPQCost() and so on. Thus, the method will work for any derived class with no mdification; however, being virtual it can be re-implemented for maximum efficiency if desired.

References CQKnPClass::KNPLBnd(), CQKnPClass::KNPLCost(), CQKnPClass::KNPQCost(), CQKnPClass::KNPUBnd(), CQKnPClass::KNPVlm(), and CQKnPClass::n.

Referenced by CQKnPClass::KNPn().

virtual void ChgLCosts	(	const double *	csts,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

Change the linear cost coefficients that are:

listed in into the vector of indices nms (ordered in increasing sense and Inf<int>()-terminated),
and whose name belongs to the interval [ strt , min( stp , KNPn() ) ).

That is, if strt <= nms[ i ] < stp, then the coefficient of the nms[ i ]-th item will be changed reading from csts[ i ]. If nms == 0 (as the default), all the entries in the given range will be changed.

Referenced by CQKnPClass::KNPn().

virtual void ChgQCosts	(	const double *	csts,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

Change the quadratic cost coefficients that are:

listed in into the vector of indices nms (ordered in increasing sense and Inf<int>()-terminated),
and whose name belongs to the interval [ strt , min( stp , KNPn() ) ).

That is, if strt <= nms[ i ] < stp, then the coefficient of the nms[ i ]-th item will be changed reading from csts[ i ]. If nms == 0 (as the default), all the entries in the given range will be changed (see above).

Referenced by CQKnPClass::KNPn().

virtual void ChgLCost	(	int	i,
		const double	cst
	)

pure virtual

Change the linear cost coefficient of item i to cst.

Referenced by CQKnPClass::KNPn().

virtual void ChgQCost	(	int	i,
		const double	cst
	)

pure virtual

Change the quadratic cost coefficient of item i to cst.

Referenced by CQKnPClass::KNPn().

virtual void ChgLBnds	(	const double *	bnds,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

Change the item lower bounds that are:

listed in into the vector of indices nms (ordered in increasing sense and Inf<int>()-terminated),
and whose name belongs to the interval [ strt , min( stp , KNPn() ) ).

That is, if strt <= nms[ i ] < stp, then the bounds of the nms[ i ]-th item will be changed reading from bnds[ i ]. If nms == 0 (as the default), all the entries in the given range will be changed.

Referenced by CQKnPClass::KNPn().

virtual void ChgUBnds	(	const double *	bnds,
		const int *	nms = `0`,
		int	strt = `0`,
		int	stp = `Inf< int >()`
	)

pure virtual

Change the item upper bounds that are:

listed in into the vector of indices nms (ordered in increasing sense and Inf<int>()-terminated),
and whose name belongs to the interval [ strt , min( stp , KNPn() ) ).

That is, if strt <= nms[ i ] < stp, then the bounds of the nms[ i ]-th item will be changed reading from bnds[ i ]. If nms == 0 (as the default), all the entries in the given range will be changed.

Referenced by CQKnPClass::KNPn().