KnpsFiOrcl Class Reference
Instantiation of FiOracle for Knapsack Lagrangian relaxation of FC-MMFC. More...
#include <KnpsFiOrcl.h>
Inheritance diagram for KnpsFiOrcl:
Public Member Functions | |
| bool | NewGi (cIndex wFi=Inf< Index >()) |
| The subgradients are calculated using the following formula:
. More... | |
Constructor | |
| KnpsFiOrcl (Graph *g, istream *iStrm=0) | |
| Constructor of the class. More... | |
| void | SetFiLog (ostream *outs=0, const char lvl=0) |
| lvl controls the "level of verbosity" of the code. More... | |
| void | SetMaxName (cIndex MxNme=0) |
| void | SetAggregate (bool agg=true) |
| Set aggregation option. More... | |
Reading other results | |
| HpNum | GetLowerBound (cIndex wFi=Inf< Index >()) |
| void | SetLowerBound (HpNum lowB=Inf< HpNum >()) |
| FiStatus | GetFiStatus (Index wFi=Inf< Index >()) |
Reading the data of the problem | |
| void | GetCosts (CRow Csts, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| void | GetICaps (FRow ICps, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| void | GetMCaps (FRow MCps, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| HpNum | GetGlobalLipschitz (cIndex wFi=Inf< Index >()) |
Adding / removing / changing data | |
| void | Deleted (cIndex i=Inf< Index >()) |
| void | Aggregate (cHpRow Mlt, cIndex_Set NmSt, cIndex Dm, cIndex NwNm) |
| void | ChgCosts (cCRow NwCsts, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| void | ChgICaps (cFRow NwICps, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| void | ChgMCaps (cFRow NwMCps, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| void | ChgIntVar (cIndex k=Inf< Index >(), bool IntVld=true, cIndex_Set nms=0, Index strt=0, Index stp=Inf< Index >()) |
Destructor | |
| virtual | ~KnpsFiOrcl () |
 Public Member Functions inherited from FiOracle | |
| virtual NDOSolver * | GetNDOSolver (void) |
| This method allows to read back the pointer to the NDOSolver that has been passed to the FiOracle through SetNDOSolver() [see above], if any. More... | |
| FiOracle (void) | |
| Constructor of the class: takes no arguments, since everything that concerns the real evaluation of the function must be done in derived classes, which will have their parameters. More... | |
| virtual void | SetNDOSolver (NDOSolver *NwSlvr=0) |
| This method is meant to pass to the FiOracle a pointer to the NDOSolver object that is using it, and that must be warned if the function Fi changes. More... | |
| virtual void | SetFiTime (const bool TimeIt=true) |
| SetFiTime() allocates an OPTtimers object [see OPTtypes.h] that should be used for timing the calls to relevant methods of the class. More... | |
| virtual void | SetMaxName (cIndex MxNme=0) |
| In some cases, an optimal solution of the dual problem (D) [see the general notes] is a mostly welcome thing; typically, this solution is given in terms of convex (nonnegative) multipliers which form 0 out of a set of subgradients (linear constraints) generated during the run of a NDO algorithm [see ReadMult() in NDOSlver.h]. More... | |
| virtual Index | GetNumVar (void) const |
| Returns the number of variables of the function, i.e., the (maximum) size of the vectors to be passed to SetLambda() and SetLamBase() [see below]. More... | |
| virtual Index | GetMaxNumVar (void) const |
| This method provides the only explicit support – except for the return value `kFiChgd' of GetFiStatus() [see below] – of the class FiOracle for the case where the function Fi changes over time. More... | |
| virtual Index | MaxNConst (void) |
| GetMaxN() returns the number of constraints. More... | |
| virtual bool | IsFiContinuous (cIndex NrFi=Inf< Index >()) |
| Returns true if the function is continuous. More... | |
| virtual bool | IsFiConvex (cIndex NrFi=Inf< Index >()) |
| Returns true if the function is continuous. More... | |
| virtual bool | HasGi (cIndex NrFi=Inf< Index >()) |
| Returns true if the oracle is able to provide first-order information about the function. More... | |
| virtual bool | IsGiContinuous (cIndex NrFi) |
| Returns true if the first-order information of the function [see HasGi() above] is continuous, i.e., the function is differentiable. More... | |
| virtual bool | HasH (cIndex NrFi) |
| Returns true if the oracle is able to provide second-order information about the function; for this to happen, (the corresponding) HasGi() also has to return true, that is, an oracle being able to provide second-order information is also necessarily able to provide first-order information. More... | |
| virtual bool | IsHContinuous (cIndex NrFi) |
| Returns true if the second-order information of the function [see HasH() above] is continuous, i.e., the function is twice differentiable. More... | |
| virtual Index | GetMaxName (void) const |
| Returns the maximum number of dual information stored in the FiOracle(), as set by the lastes call to SetMaxName(). More... | |
| virtual HpNum | GetMinusInfinity (void) |
| The function Fi to be minimized may be unbounded below, i.e., its infimum may be - INF. More... | |
| virtual Index | GetMaxNZ (cIndex wFi=Inf< Index >()) const |
| The subgradients returned by the FiOracle may happen to be very "sparse", i.e., containing very few nonzeroes; sometimes, the maximum number of nonzeroes is known in advance. More... | |
| virtual Index | GetMaxCNZ (cIndex wFi=Inf< Index >()) const |
| This method has the same meaning as GetMaxNZ() [see above], but it is about the sparsity of constraints rather than subgradients, as the two may be different. More... | |
| virtual bool | GetUC (cIndex i) |
| The variables of the function may be either constrained in sign, i.e., required to be nonnegative, or unconstrained; if Fi is a Lagrangian function, for instance, constrained variables correspond to inequality constraints while unconstrained variables correspond to equality constraints. More... | |
| virtual LMNum | GetUB (cIndex i) |
| For some of the variables of the function, an upper bound on the optimal value may be known. More... | |
| virtual LMNum | GetBndEps (void) |
| When some of the variables are declared by the FiOracle either to be nonnegative [see GetUC() above] or to possess a finite upper bound [see GetUB() above], the NDO algorithm should take care to only provide values for these variables which satisfy 0 <= Lambda[ i ] <= GetUB( i ) in the points it intends to probe the function in [see SetLambda() below]. More... | |
| virtual HpNum | GetGlobalLipschitz (cIndex wFi=Inf< Index >()) |
| Returns the Lipschitz constant. More... | |
| virtual Index | GetBNC (cIndex wFi) |
| Returns the number of variables of the "easy" linear problem which describes Fi[ wFi ], that is, the number of columns of the matrices B[ wFi ] and A[ wFi ] and the lenght of the vectors x[ wFi ], c[ wFi ], l[ wFi ] and u[ wFi ]. More... | |
| virtual Index | GetBNR (cIndex wFi) |
| Returns the number of rows of the matrix B[ wFi ] and the lenght of the vectors d[ wFi ] and e[ wFi ]; GetBNR( wFi ) can return 0 if only "box" constraints are imposed on the variables x[ wFi ]. More... | |
| virtual Index | GetBNZ (cIndex wFi) |
| Returns the number of nonzeroes in the matrix B[ wFi ]; this is clearly 0 if GetBNR( wFi ) == 0. More... | |
| virtual void | GetBDesc (cIndex wFi, int *Bbeg, int *Bind, double *Bval, double *lhs, double *rhs, double *cst, double *lbd, double *ubd) |
| Returns a description of the matrix B[ wFi ] and of the vectors d[ wFi ], e[ wFi ], c[ wFi ], l[ wFi ] and u[ wFi ]. More... | |
| virtual Index | GetANZ (cIndex wFi, cIndex strt=0, Index stp=Inf< Index >()) |
| Returns the number of nonzeroes in the matrix A[ wFi ] (whose number of columns is GetBNC( wFi ) and whose number of rows is GetNumVar()); more precisely, it returns the number of nonzeroes in the submatrix of A[ wFi ] containing all the rows with indices between start and min( stp , GetNumVar() ) - 1 (corresponding to the variables with those "names"). More... | |
| virtual void | GetADesc (cIndex wFi, int *Abeg, int *Aind, double *Aval, cIndex strt=0, Index stp=Inf< Index >()) |
| Return a description of the submatrix of A[ wFi ] containing all the rows with indices between start and min( stp , GetNumVar() ) - 1; the meaning of Abeg, Aind and Aval is analogous to that of Bbeg, Bind and Bval in GetBDesc() [see above]. More... | |
| virtual void | SetLamBase (cIndex_Set LmbdB=0, cIndex LmbdBD=0) |
| The "format" of the vector Lambda set by SetLambda() [see above] depends on the argument LamB passed to SetLamBase(). More... | |
| virtual HpNum | Fi (cIndex wFi=Inf< Index >())=0 |
| This method must return the value of the function Fi to be minimized in the point Lmbd set by SetLambda() and SetLamBase() [see above]. More... | |
| virtual bool | NewGi (cIndex wFi=Inf< Index >()) |
| This method must be called to ask the FiOracle whether it can produce a "new" item corresponding to the point Lambda set by SetLambda() and SetLamBase() [see above]. More... | |
| virtual Index | GetGi (SgRow SubG, cIndex_Set &SGBse, cIndex Name=Inf< Index >(), cIndex strt=0, Index stp=Inf< Index >())=0 |
| GetGi() [and GetVal(), see below] can be used to query information about the items. More... | |
| virtual HpNum | GetVal (cIndex Name=Inf< Index >()) |
| GetVal() [and GetGi(), see above] can be used to query information about the items. More... | |
| virtual void | SetGiName (cIndex Name) |
| After that a new item has been produced, i.e., a call to NewGi() returned true, and that (possibly) GetGi() / GetVal() have been used to retrieve information about it, the NDO solver can use SetGiName() to tell the FiOracle that a "name" has been assigned to that new item by NDO solver. More... | |
| virtual HpNum | GetLowerBound (cIndex wFi=Inf< Index >()) |
| In some cases, a Lower Bound on the minimal value of Fi is known; if Fi is a Lagrangian function, for instance, the objective function value c( x ) of any dual feasible solution x (s.t. More... | |
| virtual FiStatus | GetFiStatus (Index wFi=Inf< Index >()) |
| GetFiStatus() returns the internal status of the FiOracle object. More... | |
| void | FiTime (double &t_us, double &t_ss) |
| If this method is called within any of the methods of the class that are "actively timed" (this depends on the subclasses), it returns the user and sistem time (in seconds) since the start of that method. More... | |
| double | FiTime (void) |
| As FiTime( double & , double & ) [see above], except that returns the total (system + user ) time. More... | |
| virtual void | Deleted (cIndex i=Inf< Index >()) |
| If so instructed by SetMaxName() [see above], the FiOracle should keep "dual" information attached to the subgradients/constraints produced [see GetGi() above]. More... | |
| virtual void | Aggregate (cHpRow Mlt, cIndex_Set NmSt, cIndex Dm, cIndex NwNm) |
| Many NDO algorithms perform operations on the subgradients that they obtain from the FiOracle; the most common operation is taking linear or convex combinations of some subgradients/constraints. More... | |
| virtual | ~FiOracle () |
| Public Member Functions inherited from MMCFClass | |
| MMCFClass (void) | |
| virtual void | SetMMCFLog (ostream *outs=0, const char lvl=0) |
| void | SetMMCFTime (bool TimeIt=true) |
| virtual void | SetOptEps (const double OE=0) |
| virtual void | SetFsbEps (const double FE=0) |
| In many cases, only an "approximate" solution of the problem is possible; alternatively, only an "approximate" solution may be required for the purposes of the caller (in order to save time). More... | |
| virtual void | SetSubP (cIndex ws=Inf< Index >()) |
| virtual FONumber | GetUpprBnd (bool &HvSol) |
| virtual FONumber | GetLwrBnd (bool &HvSol) |
| These methods have to return any known Upper/Lower Bound on the optimal value of the "whole" problem (+/-INF are clearly always a possibility). More... | |
| virtual void | SetFlwSol (FRow Flw=0, Index_Set Bse=0, cIndex wf=Inf< Index >()) |
| virtual void | SetMFlwSol (MFRow Flw=0, Index_Set Bse=0, cIndex wf=Inf< Index >()) |
| virtual void | SetXtrSol (Row Xtr=0, Index_Set Bse=0) |
| Set[M]FlwSol() and SetXtrSol() are meant to pass to the object pointers to the memory where (respectively) a flow solution and an extra variables solution (the "primal information") have to be, along with "instructions" about their "format". More... | |
| virtual bool | GetUBSol (void) |
| Called after SolveMMCF() and Set[[M]Flw/Xtr]Sol(), these methods write in the memory provided for the purpose respectively the "optimal" primal solution of the problem and the primal solution of the "whole" problem corresponding to the Upper Bound, according to the required "style" [see Set[[M]Flw/Xtr]Sol()]. More... | |
| virtual bool | PSolIsFNumber (void) |
| virtual bool | UBSolIsFNumber (void) |
| These methods tell if the primal solutions (to be retrieved with GetPSol()) and the upper bound solutions (to be retrieved with GetUBSol()) are of type `FNumber' rather than `MFNumber'. More... | |
| virtual void | SetNPot (CRow NPt=0, cIndex wd=Inf< Index >()) |
| virtual void | SetRCst (CRow RCs=0, cIndex wd=Inf< Index >()) |
| virtual void | SetMCCst (CRow MCs=0) |
| virtual void | SetXtrRC (Row XRC=0) |
| virtual void | SetXtrDV (Row XDV=0) |
| SetNPot(), SetRCst(), SetMCCst(), SetXtrRC() and SetXtrDV() are meant to pass to the object pointers to the memory where, respectively,. More... | |
| virtual bool | GetLBSol (void) |
| Called after SolveMMCF() and Set[NPot/RCst/MCCst/XtrRC/XtrDV](), these methods write in the memory provided for the purpose respectively the "optimal" dual solution of the problem and the dual solution of the "whole" problem corresponding to the Lower Bound, according to the required "style". More... | |
| void | TimeMMCF (double &t_us, double &t_ss) |
| double | TimeMMCF (void) |
| If these methods are called within any of the methods of the class that are "actively timed" (this depends on the subclasses), they return respectively the user and sistem time and the total time (in seconds) since the start of that method. More... | |
| Index | NrComm (void) |
| Index | NrNodes (void) |
| Index | NrArcs (void) |
| virtual Index | NrXtrVrs (void) |
| virtual Index | NrXtrCnst (void) |
| virtual Index | NrSubP (void) |
| virtual void | GetXtrCsts (CRow XtrCs, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| virtual void | ChgXtrCsts (cCRow NwXtrCs, cIndex_Set nms=0, cIndex strt=0, Index stp=Inf< Index >()) |
| virtual void | CloseArcs (cIndex_Set whch)=0 |
| virtual void | OpenArcs (cIndex_Set whch)=0 |
| Respectively "Close" and "Open" the arcs indicated in whch, that must point to a vector of indices in [ 0 . More... | |
| virtual void | AddExtraVars (cIndex NXV, cCRow XCst=0, cFRow XUb=0, cFRow XLb=0, bool IntVar=false, cIndex_Set nms=0) |
| virtual void | AddExtraConstr (cIndex NXC, int *IBeg, int *Indx, double *Vals, cFRow XLr=0, cFRow XUr=0) |
| virtual | ~MMCFClass () |
Protected Attributes | |
Algorithmic parameters | |
| HpNum | Eps |
| Precision for some calculations. | |
| bool | Aggrgtd |
| Agreggation flag. | |
Instance data | |
| Index_Set | Startn |
| Topology of the graph: starting ... | |
| Index_Set | Endn |
| ... and ending node of each arc | |
| CRow | Costs |
| Array of unit costs. More... | |
| CRow | XtrCosts |
| Array of design costs. More... | |
| CRow | Capacities |
| Array of individual capacities. More... | |
| FRow | TotCap |
| Array of mutual capacity for the arcs. | |
| FRow | Deficits |
| deficits | |
| HpNum | LowerBound |
| A (coarse) lower bound on the value of Fi. | |
Solutions data | |
| FRow | FSolution |
| Value of the "actual" flow solution. | |
| Index | SolWFi |
| Which subproblem belongs last gi created. | |
| Index_Set | OldWFi |
| Which subproblem belongs the solution. | |
| FRow * | OldFSols |
| History of subgradients (Flow Solution). | |
| bool | DoAggregation |
| if true, do the aggregation | |
| HpRow | FiLmbd |
| Fi[ k ]( Lambda ) | |
| Protected Attributes inherited from FiOracle | |
| NDOSolver * | Slvr |
| (pointer to) the NDO solver that is currently using this oracle | |
| Index | NumVar |
| (current) number of variables if Fi() | |
| Index | MaxName |
| maximum name to be used in SetGiName() | |
| cLMRow | Lambda |
| (pointer to) the point where Fi() has to be evaluated | |
| cIndex_Set | LamBase |
| (pointer to) the set of indices of nonzeroes if Lambda[] is in "sparse" format. More... | |
| Index | LamBDim |
| length of LamBase[] | |
| bool | LHasChgd |
| true if Lambda has changed since the last call to NewGi() | |
| ostream * | FiLog |
| the output stream object for log purposes | |
| char | FiLLvl |
| the "level of verbosity" of the log | |
| OPTtimers * | Fit |
| OPTtimer for timing purposes. | |
| Protected Attributes inherited from MMCFClass | |
| Index | NArcs |
| Number of Arcs of the graph. | |
| Index | NNodes |
| Number of Nodes of the graph. | |
| Index | NComm |
| Number of Commodities. | |
| Index | XtrVrs |
| Number of "eXtra" Variables. | |
| Index | XtrCnst |
| Number of "eXtra" Constraints. | |
| Index | NSubPr |
| into how many SubProblems the MMCF can be divided | |
| FONumber | OptEps |
| an OptEps-optimal solution is required | |
| FONumber | FsbEps |
| FsbEps is the max allowed violation of constraints. | |
| Index | WhchSP |
| WhchSP tells which subproblem is one referring to. | |
| FRow | FSol |
| pointer to the memory of the Flow Solution | |
| MFRow | MFSol |
| as above, but of the MFNumber type | |
| Index_Set | FBse |
| if FBse != 0, then it must be "sparse" | |
| Index | WhchFS |
| WhchFS tells its "type" of the Flow Solution. | |
| Row | XSol |
| pointer to the memory of the "extra" solution | |
| Index_Set | XBse |
| if XBse != 0, then it must be "sparse" | |
| CRow | NPot |
| pointer to the memory of the Node Potentials (dual costs for the Flow Conservation constraints (1.k)) | |
| Index | WhchNP |
| WhchNP tells its "type" of the Node Potentials. | |
| CRow | RCst |
| pointer to the memory of the flow reduced costs (dual costs for the bound constraints (2.k)) | |
| Index | WhchRC |
| WhchRC tells its "type" of the flow reduced costs. | |
| CRow | MCst |
| pointer to the memory of the dual costs for the Mutual Capacity constraints (3) | |
| Row | XtDV |
| pointer to the memory of the dual costs for the "extra" constraints (4) | |
| Row | XtRC |
| pointer to the memory of the reduced costs for the "extra" variables (dual costs for constraints (5)) | |
| ostream * | MMCFLog |
| the output stream object | |
| char | MMCFLLvl |
| the "level of verbosity" of the log | |
| OPTtimers * | MMCFt |
| mainly the MMCFSolve() time, probably | |
Variables management related | |
| Index_Set | SGBse1 |
| format of Subgradient | |
| Bool_Vec | SlvP |
| true if the Lagrangian problem has been solved | |
| Bool_Vec | LsHasChgd |
| true if Lambda has changed since the last call to NewGi() | |
Additional Inherited Members | |
| Public Types inherited from FiOracle | |
| Public Types inherited from MMCFClass | |
| typedef unsigned int | Index |
| index of a node or arc ( >= 0 ) | |
| typedef Index * | Index_Set |
| set (array) of indices | |
| typedef const Index | cIndex |
| a read-only index | |
| typedef cIndex * | cIndex_Set |
| read-only index array | |
| typedef double | FNumber |
| type of arc flow | |
| typedef FNumber * | FRow |
| vector of flows | |
| typedef const FNumber | cFNumber |
| a read-only flow | |
| typedef cFNumber * | cFRow |
| read-only flow array | |
| typedef double | CNumber |
| type of arc flow cost | |
| typedef CNumber * | CRow |
| vector of costs | |
| typedef const CNumber | cCNumber |
| a read-only cost | |
| typedef cCNumber * | cCRow |
| read-only cost array | |
| typedef double | MFNumber |
| a Multicommodity flow variable | |
| typedef MFNumber * | MFRow |
| vector of Multicommodity flows | |
| typedef const MFNumber | cMFNumber |
| a read-only Multicommodity flow | |
| typedef cMFNumber * | cMFRow |
| read-only Multicommodity array | |
| typedef double | FONumber |
| type of the objective function: has to hold sums of products of MFNumber(s) by CNumber(s) | |
| typedef const FONumber | cFONumber |
| a read-only o.f. value | |
| typedef double | Number |
| an "extra" variable | |
| typedef Number * | Row |
| an "extra" variable array | |
| typedef const Number | cNumber |
| a read-only Number | |
| typedef cNumber * | cRow |
| read-only Number array | |
Detailed Description
Instantiation of FiOracle for Knapsack Lagrangian relaxation of FC-MMFC.
This class instantiates the FiOracle interface [see FiOracle.h] to solve the knapsack Lagrangian relaxation of the (Fixed-Charge) Multicommodity Min Cost Flow Problem ((FC-)MMCF). The problem formulation is below:
![\[ \phi(\upsilon)= \min \sum_{k \in K} \sum_{(i,j) \in A} \left( c_{ij}^k + \upsilon_i^k - \upsilon_j^k \right) x_{ij}^k + \sum_{(i,j) \in A} f_{ij}y_{ij} - \sum_{n \in N} \sum_{k \in K} \left( \upsilon_i^k - b_i^k \right) \]](form_17.png)
![\[ \sum_{k \in K} x_{ij}^k \leq u_{ij} y_{ij} \quad,\quad (i,j) \in A \]](form_18.png)
![\[ 0 \leq x_{ij}^k \leq u_{ij}^k y_{ij} \quad,\quad (i,j) \in A, k \in K \]](form_19.png)
![\[ y_{ij} \in \{0,1\} \quad,\quad (i,j) \in A \]](form_20.png)
The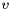 
vector is the Lambda values described in the FiOracle interface. They are dual variables associated to the relaxed flow conservation constraints.
Constructor & Destructor Documentation
| KnpsFiOrcl | ( | Graph * | g, |
| istream * | iStrm = 0 |
||
| ) |
Constructor of the class.
The parameter `iStrm', if provided, is taken as a pointer to a istream from which the algorithmic parameters for the knapsack relaxation are sequentially read in the following order. Each parameter must be placed at the beginning of a separate line, max 255 characters long, with all the rest of the line up to the first newline character (apart from a separating whitespace) being available for comments. Any line whose first character is '#' and any blank line is ignored. If 0 is passed, the file ends before reaching a given parameter, or some parameter is in the wrong format, each non-specified parameter is given a default value, shown in [] below.
`iStrm' is passed to the constructor of FiOracle [see FiOracle.h], which reads the general algorithmic parameters out of it; since the constructor KnpsFiOrcl is executed after the one of FiOracle, the following parameters specific for the SubGrad have to be found in the stream after those of the base class:
- agg [0] 1 if the function is considered as one function, 0 if decomposed
- Eps [1e-6] precision of Fi()
- DoAggregation [0] 1 if the variables generation is adopted, 0 otherwise.
Member Function Documentation
|
virtual |
lvl controls the "level of verbosity" of the code.
The first four bits of lvl have the following meaning:
0 => no log at all (also assumed if log = 0);
>0 => "basic" log: only the errors are reported;
Reimplemented from FiOracle.
| void SetAggregate | ( | bool | agg = true | ) |
Set aggregation option.
Tells if the FiOracle works with Fi aggregated or disaggregated.
The subgradients are calculated using the following formula:
![\[ gi(\upsilon_i^k) = \sum_{(i,j) \in A} \left( x_{ij}^k - \sum_{(j,i)\in A}x_{ji}^k \right) - b_i^k \]](form_22.png)
.
Member Data Documentation
|
protected |
Array of unit costs.
Each entry corresponds to the cost of one unit of flow of one commodity traversing one arc. For arc j and commodity k, this cost is OrigCosts[ k * m + j ], where m stands for the total number of arcs.
|
protected |
Array of design costs.
Each entry is associated with the fixed cost of the corresponding arc being used.
|
protected |
Array of individual capacities.
Each entry OrigCapacities[ k * m + j ] corresponds to the maximum flow of a given commodity, k, allowed in a given arc, j.
