This class instantiates the FiOracle interface [see FiOracle.h] to solve the flow Lagrangian relaxation of the (Fixed-Charge) Multicommodity Min Cost Flow Problem ((FC-)MMCF), possibly with "easy" components for the design variables. More...
#include <FlwFiOrcl.h>
Public Types | |
Public Types | |
 Public Types inherited from FiOracle |
Public Member Functions | |
| bool | NewGi (cIndex wFi=Inf< Index >()) |
| The first time NewGi() is called, it computes the "true" subgradients. More... | |
| void | GetPar (const int wp, bool &value) |
| Read the current value of the "bool" parameters of the FlwFiOracle. More... | |
| void | GetPar (const int wp, Index &value) |
| Read the current value of the "int" parameters of the FlwFiOracle [see above]. More... | |
| virtual | ~FlwFiOrcl () |
| Destructor of the class: it must be virtual. | |
Constructor | |
| FlwFiOrcl (Graph *g, istream *iStrm=NULL) | |
| Constructor of the class. More... | |
Other initializations | |
| void | SetFiLog (ostream *outs=0, const char lvl=0) |
| lvl controls the "level of verbosity" of the code. More... | |
| void | SetMaxName (cIndex MxNme) |
| void | SetAggregate (bool aggrgt=true) |
| Set aggregation option. More... | |
| void | SetRelax (const char sp4= 'w', bool YiE=false, cIndex sp1=0, cIndex sp2=0, cIndex sp3=0) |
| Set relaxation of Individual Capacities or off. More... | |
| void | SetInitialSet (Index_Set Bse) |
| Set the initial dictionary. More... | |
| void | SetEasy (bool YIsE=false) |
| Set Easy option. More... | |
Reading other results | |
| HpNum | GetLowerBound (cIndex wFi=Inf< Index >()) |
| void | SetLowerBound (HpNum lowB=Inf< HpNum >()) |
| FiStatus | GetFiStatus (Index wFi=Inf< Index >()) |
| double | AddTime (void) |
| Returns the user + system time (in seconds) spent during the execution for adding of new beta variables. More... | |
| double | RemTime (void) |
| As AddTime() [see above], it returns the time spent for removing the beta variables. More... | |
| bool | checkSolution (void) |
| Public Member Functions inherited from FiOracle | |
| virtual NDOSolver * | GetNDOSolver (void) |
| This method allows to read back the pointer to the NDOSolver that has been passed to the FiOracle through SetNDOSolver() [see above], if any. More... | |
| FiOracle (void) | |
| Constructor of the class: takes no arguments, since everything that concerns the real evaluation of the function must be done in derived classes, which will have their parameters. More... | |
| virtual void | SetNDOSolver (NDOSolver *NwSlvr=0) |
| This method is meant to pass to the FiOracle a pointer to the NDOSolver object that is using it, and that must be warned if the function Fi changes. More... | |
| virtual void | SetFiTime (const bool TimeIt=true) |
| SetFiTime() allocates an OPTtimers object [see OPTtypes.h] that should be used for timing the calls to relevant methods of the class. More... | |
| virtual void | SetMaxName (cIndex MxNme=0) |
| In some cases, an optimal solution of the dual problem (D) [see the general notes] is a mostly welcome thing; typically, this solution is given in terms of convex (nonnegative) multipliers which form 0 out of a set of subgradients (linear constraints) generated during the run of a NDO algorithm [see ReadMult() in NDOSlver.h]. More... | |
| virtual Index | MaxNConst (void) |
| GetMaxN() returns the number of constraints. More... | |
| virtual bool | IsFiContinuous (cIndex NrFi=Inf< Index >()) |
| Returns true if the function is continuous. More... | |
| virtual bool | IsFiConvex (cIndex NrFi=Inf< Index >()) |
| Returns true if the function is continuous. More... | |
| virtual bool | HasGi (cIndex NrFi=Inf< Index >()) |
| Returns true if the oracle is able to provide first-order information about the function. More... | |
| virtual bool | IsGiContinuous (cIndex NrFi) |
| Returns true if the first-order information of the function [see HasGi() above] is continuous, i.e., the function is differentiable. More... | |
| virtual bool | HasH (cIndex NrFi) |
| Returns true if the oracle is able to provide second-order information about the function; for this to happen, (the corresponding) HasGi() also has to return true, that is, an oracle being able to provide second-order information is also necessarily able to provide first-order information. More... | |
| virtual bool | IsHContinuous (cIndex NrFi) |
| Returns true if the second-order information of the function [see HasH() above] is continuous, i.e., the function is twice differentiable. More... | |
| virtual Index | GetMaxName (void) const |
| Returns the maximum number of dual information stored in the FiOracle(), as set by the lastes call to SetMaxName(). More... | |
| virtual HpNum | GetMinusInfinity (void) |
| The function Fi to be minimized may be unbounded below, i.e., its infimum may be - INF. More... | |
| virtual Index | GetMaxNZ (cIndex wFi=Inf< Index >()) const |
| The subgradients returned by the FiOracle may happen to be very "sparse", i.e., containing very few nonzeroes; sometimes, the maximum number of nonzeroes is known in advance. More... | |
| virtual Index | GetMaxCNZ (cIndex wFi=Inf< Index >()) const |
| This method has the same meaning as GetMaxNZ() [see above], but it is about the sparsity of constraints rather than subgradients, as the two may be different. More... | |
| virtual bool | GetUC (cIndex i) |
| The variables of the function may be either constrained in sign, i.e., required to be nonnegative, or unconstrained; if Fi is a Lagrangian function, for instance, constrained variables correspond to inequality constraints while unconstrained variables correspond to equality constraints. More... | |
| virtual LMNum | GetUB (cIndex i) |
| For some of the variables of the function, an upper bound on the optimal value may be known. More... | |
| virtual LMNum | GetBndEps (void) |
| When some of the variables are declared by the FiOracle either to be nonnegative [see GetUC() above] or to possess a finite upper bound [see GetUB() above], the NDO algorithm should take care to only provide values for these variables which satisfy 0 <= Lambda[ i ] <= GetUB( i ) in the points it intends to probe the function in [see SetLambda() below]. More... | |
| virtual HpNum | GetGlobalLipschitz (cIndex wFi=Inf< Index >()) |
| Returns the Lipschitz constant. More... | |
| virtual Index | GetBNC (cIndex wFi) |
| Returns the number of variables of the "easy" linear problem which describes Fi[ wFi ], that is, the number of columns of the matrices B[ wFi ] and A[ wFi ] and the lenght of the vectors x[ wFi ], c[ wFi ], l[ wFi ] and u[ wFi ]. More... | |
| virtual Index | GetBNR (cIndex wFi) |
| Returns the number of rows of the matrix B[ wFi ] and the lenght of the vectors d[ wFi ] and e[ wFi ]; GetBNR( wFi ) can return 0 if only "box" constraints are imposed on the variables x[ wFi ]. More... | |
| virtual Index | GetBNZ (cIndex wFi) |
| Returns the number of nonzeroes in the matrix B[ wFi ]; this is clearly 0 if GetBNR( wFi ) == 0. More... | |
| virtual void | GetBDesc (cIndex wFi, int *Bbeg, int *Bind, double *Bval, double *lhs, double *rhs, double *cst, double *lbd, double *ubd) |
| Returns a description of the matrix B[ wFi ] and of the vectors d[ wFi ], e[ wFi ], c[ wFi ], l[ wFi ] and u[ wFi ]. More... | |
| virtual Index | GetANZ (cIndex wFi, cIndex strt=0, Index stp=Inf< Index >()) |
| Returns the number of nonzeroes in the matrix A[ wFi ] (whose number of columns is GetBNC( wFi ) and whose number of rows is GetNumVar()); more precisely, it returns the number of nonzeroes in the submatrix of A[ wFi ] containing all the rows with indices between start and min( stp , GetNumVar() ) - 1 (corresponding to the variables with those "names"). More... | |
| virtual void | GetADesc (cIndex wFi, int *Abeg, int *Aind, double *Aval, cIndex strt=0, Index stp=Inf< Index >()) |
| Return a description of the submatrix of A[ wFi ] containing all the rows with indices between start and min( stp , GetNumVar() ) - 1; the meaning of Abeg, Aind and Aval is analogous to that of Bbeg, Bind and Bval in GetBDesc() [see above]. More... | |
| virtual void | SetLamBase (cIndex_Set LmbdB=0, cIndex LmbdBD=0) |
| The "format" of the vector Lambda set by SetLambda() [see above] depends on the argument LamB passed to SetLamBase(). More... | |
| virtual HpNum | Fi (cIndex wFi=Inf< Index >())=0 |
| This method must return the value of the function Fi to be minimized in the point Lmbd set by SetLambda() and SetLamBase() [see above]. More... | |
| virtual bool | NewGi (cIndex wFi=Inf< Index >()) |
| This method must be called to ask the FiOracle whether it can produce a "new" item corresponding to the point Lambda set by SetLambda() and SetLamBase() [see above]. More... | |
| virtual Index | GetGi (SgRow SubG, cIndex_Set &SGBse, cIndex Name=Inf< Index >(), cIndex strt=0, Index stp=Inf< Index >())=0 |
| GetGi() [and GetVal(), see below] can be used to query information about the items. More... | |
| virtual HpNum | GetVal (cIndex Name=Inf< Index >()) |
| GetVal() [and GetGi(), see above] can be used to query information about the items. More... | |
| virtual void | SetGiName (cIndex Name) |
| After that a new item has been produced, i.e., a call to NewGi() returned true, and that (possibly) GetGi() / GetVal() have been used to retrieve information about it, the NDO solver can use SetGiName() to tell the FiOracle that a "name" has been assigned to that new item by NDO solver. More... | |
| virtual HpNum | GetLowerBound (cIndex wFi=Inf< Index >()) |
| In some cases, a Lower Bound on the minimal value of Fi is known; if Fi is a Lagrangian function, for instance, the objective function value c( x ) of any dual feasible solution x (s.t. More... | |
| virtual FiStatus | GetFiStatus (Index wFi=Inf< Index >()) |
| GetFiStatus() returns the internal status of the FiOracle object. More... | |
| void | FiTime (double &t_us, double &t_ss) |
| If this method is called within any of the methods of the class that are "actively timed" (this depends on the subclasses), it returns the user and sistem time (in seconds) since the start of that method. More... | |
| double | FiTime (void) |
| As FiTime( double & , double & ) [see above], except that returns the total (system + user ) time. More... | |
| virtual void | Deleted (cIndex i=Inf< Index >()) |
| If so instructed by SetMaxName() [see above], the FiOracle should keep "dual" information attached to the subgradients/constraints produced [see GetGi() above]. More... | |
| virtual void | Aggregate (cHpRow Mlt, cIndex_Set NmSt, cIndex Dm, cIndex NwNm) |
| Many NDO algorithms perform operations on the subgradients that they obtain from the FiOracle; the most common operation is taking linear or convex combinations of some subgradients/constraints. More... | |
| virtual | ~FiOracle () |
Protected Attributes | |
Algorithmic parameters | |
| HpNum | EpsFi |
| Precision for the design problem. More... | |
| HpNum | EpsCon |
| Precision for the constraints problem. | |
| bool | Aggrgtd |
| Agreggation flag. More... | |
| bool | YIsEasy |
| true if the ys are easy components. More... | |
Lagrangian data | |
| Index_Set | InvULambda |
| Inverse vocabulary of ULambda. More... | |
| Index_Set | ZLambdaCount |
| Counter of iterations with value zero for each variable. More... | |
| Index_Set | SGBse1 |
Instance data | |
| Index | MaxNumVar |
| The maximum number of variables. More... | |
| CRow | OrigCosts |
| Array of original unit costs. More... | |
| CRow | OrigXtrCosts |
| Array of original design costs. More... | |
| CRow | OrigCapacities |
| Array of original individual capacities. More... | |
| FRow | OrigTotCap |
| Array of mutual capacity for the arcs. | |
| FRow | OrigDeficits |
| Original deficits. | |
| HpNum | LowerBound |
| A (coarse) lower bound on the value of Fi. | |
Solutions data | |
| Index_Set | OldWFi |
| Witch subproblem belongs the solution. | |
| FRow * | OldFSols |
| History of subgradients (Flow Solution). | |
| Mat | OldXSols |
| History of subgradients (Extra Solution). | |
| SIndex | KOld |
| number of allocated Old Solution | |
| FRow | FSolution |
| Index | SolWFi |
| Witch subproblem belongs last gi created. | |
| Row | XSolution |
| Bool_Vec | SolvedP |
Variables management related | |
| Index | SPar1 |
| Variables addition interval. More... | |
| Index | SPar2 |
| Maximum n. More... | |
| Index | SPar3 |
| Remotion of original constraints is checked every SPar3 iterations. More... | |
| char | SPar4 |
| For specifying which kind of constraints have to be relaxed. More... | |
| Bool_Vec | LsHasChgd |
| true if Lambda has changed since the last call to NewGi() | |
| OPTtimers * | Addt |
| Timer for variables addition. | |
| OPTtimers * | Remt |
| Timer for variables deletion. | |
| Protected Attributes inherited from FiOracle | |
| NDOSolver * | Slvr |
| (pointer to) the NDO solver that is currently using this oracle | |
| Index | NumVar |
| (current) number of variables if Fi() | |
| Index | MaxName |
| maximum name to be used in SetGiName() | |
| cLMRow | Lambda |
| (pointer to) the point where Fi() has to be evaluated | |
| cIndex_Set | LamBase |
| (pointer to) the set of indices of nonzeroes if Lambda[] is in "sparse" format. More... | |
| Index | LamBDim |
| length of LamBase[] | |
| bool | LHasChgd |
| true if Lambda has changed since the last call to NewGi() | |
| ostream * | FiLog |
| the output stream object for log purposes | |
| char | FiLLvl |
| the "level of verbosity" of the log | |
| OPTtimers * | Fit |
| OPTtimer for timing purposes. | |
Detailed Description
This class instantiates the FiOracle interface [see FiOracle.h] to solve the flow Lagrangian relaxation of the (Fixed-Charge) Multicommodity Min Cost Flow Problem ((FC-)MMCF), possibly with "easy" components for the design variables.
It derives from MMCFFlwBase (and hence from MMCFClass) and uses its methods to solve the flow relaxation.
The problem formulation is:
![\[ \phi( \alpha , \beta ) = \min \left\{ \sum_{k \in K} \sum_{(i, j) \in A} \left( c_{ij}^k + \alpha_{ij} + \beta_{ij}^k \right)x_{ij}^k + \left( f_{ij} - \alpha_{ij} u_{ij} - \sum_{k \in K} \beta_{ij}^k u_{ij}^k \right) y_{ij} \right\} \]](form_5.png)
![\[ \sum_{(i, j) \in A} x_{ij}^k - \sum_{(j,i) \in A} x_{ij}^k = b_i^k \quad,\quad i \in N , k \in K \]](form_6.png)
![\[ 0 \leq x_{ij}^k \leq u_{ij}^k \quad,\quad (i, j) \in A , k \in K \]](form_7.png)
![\[ y_{ij} \in \{0, 1\} \quad,\quad (i, j) \in A \]](form_8.png)
The pair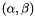 
is the Lambda vector described in the FiOracle interface. The 
's are dual variables associated to the relaxed mutual capacity constraints. These variables are always used. The 
's are dual variables associated to the relaxed individual capacity constraints. These variables only are used if SetICapRelax( true ) is called.
Member Enumeration Documentation
| enum FlwParam |
Public enum for handling the FlwFiOrcl-specific parameters in [see below].
Constructor & Destructor Documentation
Constructor of the class.
- Parameters
-
g an instance of the class Graph that defines the problem. iStrm parameters file used to read some parameters not predicted in the FiOracle interface. In particular, the following parameters are read:
- SPar1 [0] how often the check for adding variables is performed (0 = never, all variables are there from the beginning)
- SPar2 [0] a variable is removed if it has had value zero for SPar2 consecutive iterations, if 0 = no variables is removed
- SPar3 [0] how often the check form removing variable is performed
- SPar4 [w] relaxation type: 0 weak , b strong formulation and s the individual capacity constraints are the ones and only the ones involved
- YiE [0] 0: easy components are to be used 1: otherwise
- Aggrgtd [1] 0 if disaggregated master problem 1: aggregated master problem
- KOld [0] pre-set number of old solutions that are kept in memory
EpsFi [1e-6] precision for the design part
- EpsCon [1e-6] precision for the constraints
Note that the separation parameters SPar1-3 are irrelevant if the weak relaxation has been required.
Member Function Documentation
|
virtual |
lvl controls the "level of verbosity" of the code.
The first four bits of lvl have the following meaning:
0 => no log at all (also assumed if log = 0);
>0 => "basic" log: only the errors are reported;
Reimplemented from FiOracle.
| void SetAggregate | ( | bool | aggrgt = true | ) |
Set aggregation option.
Used to tell the FiOracle if it should work with Fi aggregated (true) or disaggregated (false) option.
| void SetInitialSet | ( | Index_Set | Bse | ) |
Set the initial dictionary.
Bse is the base of the current (beta) solution Thus, the dimension is not greater than
- MaxNumVar - NArcs, if there are mutual forcing capacity constraints
- MaxNumVar, if there are only individual forcing capacity constraints
| void SetEasy | ( | bool | YIsE = false | ) |
Set Easy option.
Used to tell to the FiOracle that there exist "easy" components of Fi(). By default YIsEasy has the value to false and all components are handled as "difficult".
The first time NewGi() is called, it computes the "true" subgradients.
The second time it computes (epsilon-)subgradients associated with a primal solution that is obtained by running the heuristic with the commodities ordered by decreasing demand. Every subsequent call, it computes (epsilon-)subgradients associated with primal solutions that are obtained by running the heuristic with the commodities randomly ordered. Thus, it can always be called, but it can generate repeated epsilon subgradients.
The "true" subgradients are calculated using the following formulas:
- If the disaggregated version is used:
![\[ gi^k(\alpha_{ij})=gi^k(\beta_{ij}^k)=x_{ij}^k ,\forall\: subproblem\: k \]](form_12.png)
![\[ gi^0(\alpha_{i,j})=-u_{ij}y_{ij}\]](form_13.png)
![\[ gi^0(\beta_{i,j}^k)=b_{ij}^ky_{ij}\]](form_14.png)
- If the aggregated version is used:
![\[ gi(\alpha_{i,j})=\left(sum_{k \in K}x_{ij}^k-u_{ij}y_{ij}\right) \]](form_15.png)
![\[ gi(\beta_{i,j}^k)=x_{ij}^k-b_{ij}^ky_{ij}\]](form_16.png)
| double AddTime | ( | void | ) |
Returns the user + system time (in seconds) spent during the execution for adding of new beta variables.
| double RemTime | ( | void | ) |
As AddTime() [see above], it returns the time spent for removing the beta variables.
|
inline |
Read the current value of the "bool" parameters of the FlwFiOracle.
The enum FlwParam is used (in the obvious way) for selecting the parameter to be get.
|
inline |
Read the current value of the "int" parameters of the FlwFiOracle [see above].
The enum FlwParam is used (in the obvious way) for selecting the parameter to be get.
Member Data Documentation
|
protected |
Precision for the design problem.
The design solution value is considered (y=1) only if less than or equal to -Eps. This value is set to EFnal (read from parameter input file) by the NDOSolver.
|
protected |
Agreggation flag.
Variable that defines if FlwFiOracle outputs aggregated or disaggregated information
|
protected |
true if the ys are easy components.
|
protected |
Inverse vocabulary of ULambda.
This vector contains the name of the variable beta corresponding to the position in Lambda of the index (+ NArcs) in the vector. It terminates with Inf<Index>()
|
protected |
Counter of iterations with value zero for each variable.
|
protected |
The maximum number of variables.
By default the value of this variable is equal to NrArcs() + NrArcs() * NrComm(), it means the individual capacities constrainsts are relaxed. If SetICapRelax( false ) is called then the value of the variable is NrArcs(), it means only the mutual capacity constraints are relaxed.
|
protected |
Array of original unit costs.
Each entry corresponds to the cost of one unit of flow of one commodity traversing one arc. For arc j and commodity k, this cost is OrigCosts[ k * m + j ], where m stands for the total number of arcs.
|
protected |
Array of original design costs.
Each entry is associated with the fixed cost of the corresponding arc; if OrigXtrCosts == 0, then no extra costs are defined for the instance.
|
protected |
Array of original individual capacities.
Each entry OrigCapacities[ k * m + j ] corresponds to the maximum flow of a given commodity, k, allowed in a given arc, j.
|
protected |
Variables addition interval.
Original constraints are checked every SPar1 and a variable is added for each one currently violated (0 = no adding of variables is allowed).
|
protected |
Maximum n.
of iterations each variable can be 0. If one variable is ParRemVariables iterations with value zero it's removed.
|
protected |
Remotion of original constraints is checked every SPar3 iterations.
|
protected |
For specifying which kind of constraints have to be relaxed.
